Cəbr
XI sinif
§ 1 . Funksiyanın törəməsi
1. Nöqtənin ətrafı anlayışı. Funksiyanın limitinin tərifi və limitin xassələri. Sonsuz kiçilən funksiyalar.
2. 
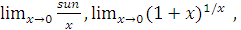limitləri
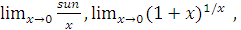limitləri
3. Funksiyanın kəsilməzliyi və kəsilməz funksiyaların xassələri. Elementar funksiyaların kəsilməzliyi.
4. Parçada kəsilməz funksiyaların aralıq qiymətləri haqqında teoremlər. İntervallar üsulu ilə bərabərsizliklər həllinin əsaslandırılması
5. Arqument və funksiyanın artımı
6. Törəmənin tərifi. Diferensiallanan funksiya. Funksiyanın diferensialı. Diferensiallanan funksiyanın kəsilmzliyi
7. Cəmin , hasilin, nisbətin və qüvvətin törəməsi.
8. Mürəkkəb funksiyanın və tərs funksiyanın törəməsi
9. Triqonometrik funksiyaların, tərs triqonometrik funksiyaların, üstlü, loqarifmik və qüvvət funksiyalarının törəmələri
§ 2. Törəmənin tətbiqləri
1. Törəmənin həndəsi mənası. Funksiyanın qrafikinə toxunan. Toxunanın tənliyi
2. Funksiyanın ikinci tərtib törəməsi
3. Törəmənin fiziki mənası
4. Törəmənin təqribi hesablamlara və fizikaya tətbiqləri
§3. Törəmənin tətbiqi ilə funksiyanın araşdırılması
1. Funksiyanın artması və azalması əlamətləri
2. Funksiyanın böhran nöqtələri. Ekstremum nöqtələri, funksiyanın ən kiçik və ən böyük qiymətləri
3. Törəmənin tətbiqi ilə funksiyanın araşdırılması və qrafikinin qurulması
4. Funksiyanın parçada ən böyük və ən kiçik qiymətlərinin tapılmasına aid məsələlər həlli
§1 . İbtidai funksiya
1. ibtidai funksiyanın tərifi. Qeyri-müəyyən inteqral
2. İbtidai funksiyanın əsas xassələri
3. İbtidai funksiyanın tapılmasının üç qaydası
4. Dəyişənin əvəz edilməsi üsulu. Hissə-hissə inteqrallama üsulu
5. Diferensial tənlik anlayışı.
§2. Müəyyən inteqral
1. Əyrixətli trapesiyanın sahəsi
2. Müəyyən inteqral. Nyuton-Leybnis düsturu. Müəyyən inteqralın xassələri
3. Müəyyən inteqralın tətbiqləri
1. Çoxluqlar cəbri
2. Permutasiyalar
3. Aranjemanlar
4. Kombinezonlar
5. Nyuton binomu. Binomun əmsallarının xassələri. Paskal üçbucağı
6. Riyazi induksiya metodu
1. Hadisə anlayışı.
2. Eyni ehtimallı hadisələr. Elementar hadisələr. Əlverişli hallar
3. Hadisələrin ehtimalı
4. Birləşmələr nəzəriyyəsi düsturlarının tətbiqi ilə sadə məsələlər həlli
§1 Birdəyişənli çoxhədli
1. Birdəyişənli çoxhədlinin kanonik şəkli. Birdəyişənli çoxhədlilər üzərində əməllər.
2. Birdəyişənli çoxhədlinin kökü. Bezu teoremi. Cəbrin əsas teoremi
3. Horner sxemi
4. Qeyri- müəyyən əmsallar üsulu
§2 . Bir neçə dəyişəni olan çoxhədlilər
1. Bir neçə dəyişəni olan çoxhədlilərin standart şəkli
2. Simmetrik çoxhədlilər
§3. Tənliklər. Tənliklər və bərabərsizliklər sistemi
1. Tənliklər anlayışı. Eynigüclü sistemlər
2. Simmetrik sistemlər. Əvəzetmə üsulu ilə simmetrik tənliklər sisteminin həlli
3. Çoxdəyişənli xətti tənliklər sisteminin həlli
4. Bərabərsizliklərin isbatına aid çalışmalar
İnformatika hazırlığı
Tam məlumat...
Ofis proqramları kursu
Tam məlumat...
Riyaziyyat dərsləri - qeydiyyat başladı
Tam məlumat...
......